ダイオードブリッジを利用することで、ACをDCに変換することができます。しかしながら、ダイオードでは、点弧タイミングを制御することができないため、電圧や電流を制御することができません。そこで、ダイオードの代わりにターンオンタイミングを制御できるサイリスタを利用します。


サイリスタの動作
サイリスタの回路記号は図1のとおりです。ダイオードにゲート端子が追加された素子となります。ゲート端子にパルスを与えることでサイリスタを導通させることができます。しかしながら、ターンオフのタイミングを制御することができず、周囲の電気回路の影響を受けることになります。
サイリスタを利用した場合の波形例を図2に示します。上から、アノード電圧、ゲート信号、サイリスタ電流です。t = 0sにてサイリスタ電流が流れていないことから分かるとおり、サイリスタではアノード電圧がプラスになった場合でも自動で導通するわけではありません。t = 0.002s付近で導通することから分かるとおり、サイリスタではゲート信号を用いてターンオンさせます。その後t = 0.01s付近にてサイリスタの導通が止まりますが、これはアノード電圧が負になったためです。このように、サイリスタは外部の電圧によりターンオフし、制御することができません。
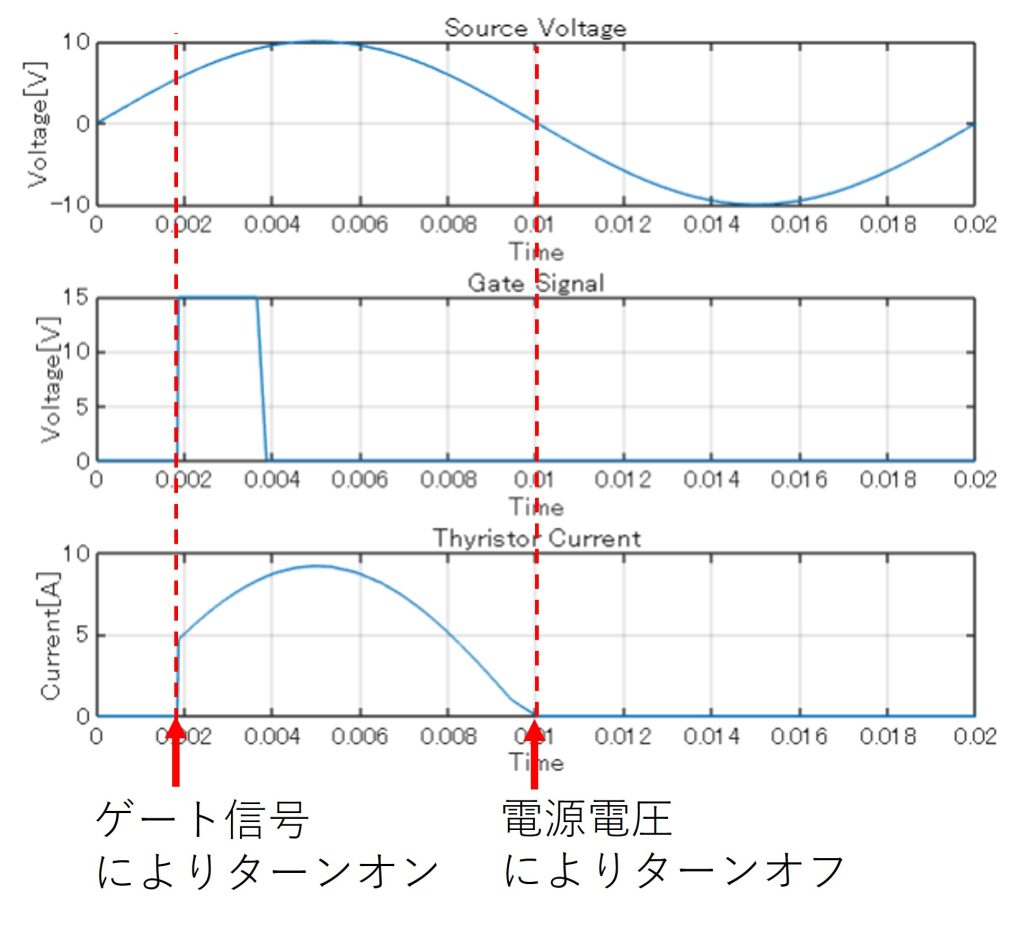
ゲート信号によりターンオンを制御できるが、ターンオフは制御できない
サイリスタを利用した三相全波整流回路の回路構成と動作
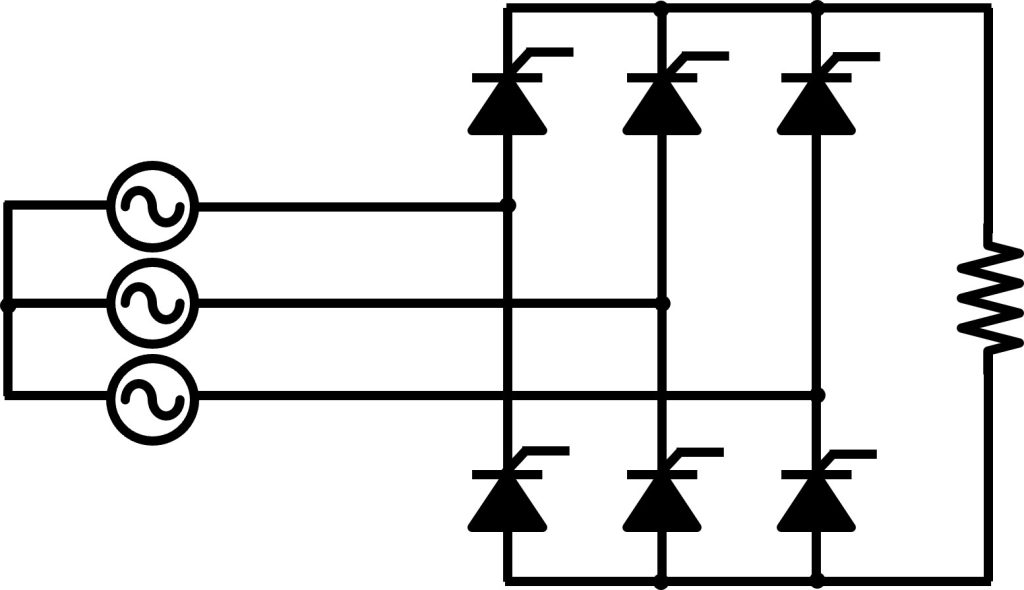
前述のサイリスタを利用した三相全波整流回路を図3に示します。ダイオードをサイリスタに置き換えた回路になります。出力電圧は、ダイオードでの三相全波整流回路と同様に上側アームと下側アームの差分になります。
サイリスタはダイオードと異なり、ターンオンタイミングを制御することが可能です。例えば、ダイオードと比較して位相を30度遅らせた場合の波形を図4に示します。上側アームの出力(Vmax)と下側アームの出力(Vmin)がダイオード整流回路と比較して遅れていることが分かります。その結果、出力波形(Vout)がダイオードの時より若干低下しています。
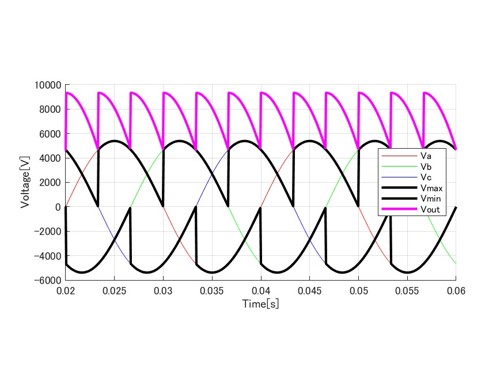
(制御角α=30°)
さらに、位相を遅らせて、90度になった場合の波形を図5に示します。各サイリスタの点弧タイミングが遅れた結果、出力波形(Vout)がダイオードの時より低下しています。実際この時の出力平均電圧は0になります。
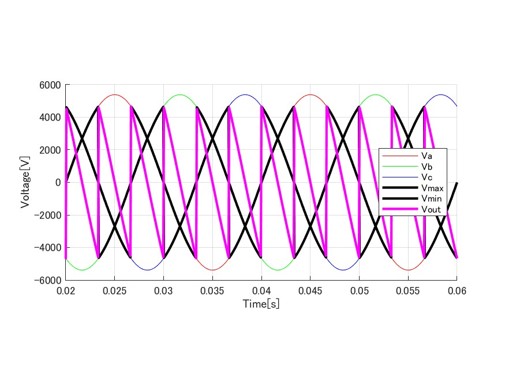
(制御角α=90°)
このようにサイリスタの三相全波整流回路では、点弧タイミングをどれだけ遅らせるかにより、出力電圧を変更することが可能です。この時の点弧タイミングの遅れを位相角や制御角などと呼び、\( \alpha \)書かれます。
サイリスタブリッジの出力電圧
図3、図4から分かるとおり、制御角\( \alpha \)より出力電圧が変化することが分かりました。ここでは、1周期の平均電圧を計算します。
出力電圧の平均電圧の一般的な計算式は次のとおりです。
$$ V_{dc} = \frac{1}{T} \int_{T_{0}}^{T+T_{0}} V_{load} d \theta $$
次に、1周期の計算として、上側アームではA相が下側アームではB相が選ばれる区間を利用します。つまり、\(T_{0}=\frac{\pi}{6}+\alpha, T=\frac{\pi}{3}+\alpha \)を代入します。
$$ V_{dc} = \frac{1}{T} \int_{T_{0}}^{T+T_{0}} V_{load} d \theta = \frac{3}{\pi} \int_{\frac{\pi}{6}+\alpha}^{\frac{\pi}{3}+\alpha} V_{load} d \theta $$
ここで\(V_{load}\)に注目します。負荷電圧はA相電圧とB相電圧の差分になります。
$$ V_{dc} = \frac{3}{\pi} \int_{\frac{\pi}{6}+\alpha}^{\frac{\pi}{3}+\alpha} \frac{\sqrt{2}}{\sqrt{3}} V_{s} {\sin \theta – \sin (\theta – \frac{2\pi}{3})}\theta $$
ここで、Vsは線間電圧を示します。また、\(\frac{1}{\sqrt{3}}\)は線間電圧を相電圧に変換するための係数、\(\sqrt{2}\)は実効値をピーク値に変換するための係数です。この式を展開すると次の結果が得られます。
$$ V_{dc} = \frac{3\sqrt{2}}{\pi} V_{s} \cos \alpha \simeq 1.35V_{s} \cos \alpha $$
この数式から分かるとおり、直流出力は制御角\( \alpha \)より制御することが可能になります。
まとめ
このページでは、サイリスタを利用した三相全波整流回路の紹介をしました。ポイントは以下のとおりです。
- サイリスタはターンオンを制御でき、ターンオフを制御できない半導体素子です。
- サイリスタによる三相全波整流回路では、ターンオンを遅らせることで電圧を制御できます。
- 遅らせる位相量のことを位相角や制御角と呼び、\( \alpha \)と表記します。

