別ページにて昇圧コンバータのシミュレーションを行い、リップルが抑制できることを紹介しました。このページでは、インダクタ電流および出力電圧のリップルの量(ピーク-ピーク)について定量的な検討を行います。
リップル量の理論式の導出
インダクタ電流と出力電圧のリップルを計算します。インダクタ電流はスイッチON時に増加しスイッチOFF時に減少、出力電圧はスイッチON時に低下しスイッチOFF時に増加します。そのため、スイッチON状態のインダクタ電流増加量、出力電圧減少量がリップルになります。そのため、半導体スイッチオン状態におけるインダクタ電流と出力電圧に注目します。
半導体スイッチオン状態の昇圧コンバータの電流経路
オン状態の昇圧コンバータの電流経路は図1のとおりです。オン状態では、インダクタ側の電流ループと出力側の電流ループが形成されています。この状態の特性を利用してリップル量を計算します。
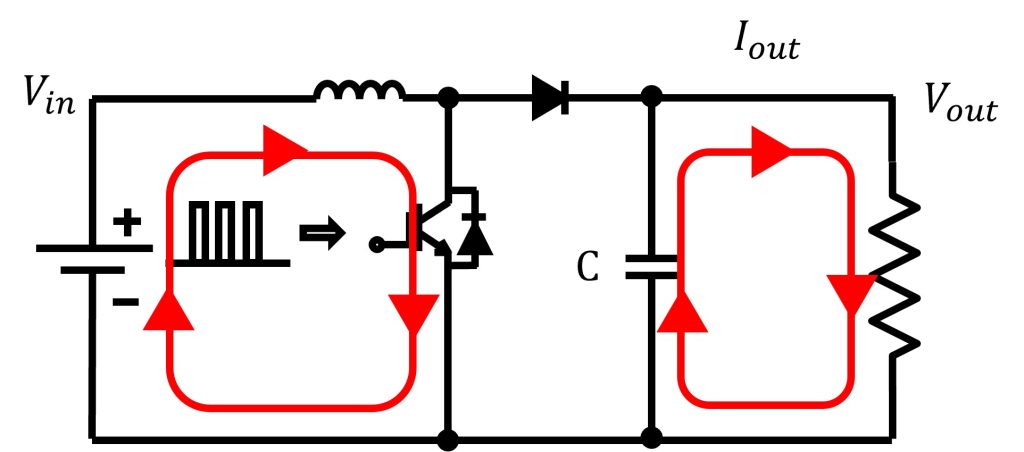
半導体スイッチがオン状態の電流経路を示す
インダクタ電流のリップル量
インダクタの電圧について、次の式が成立します。
$$ L \frac{di_{L}}{dt} = V_{in}
この式を展開すると次の式を得られます。
$$ \Delta i_{L} = \int{DT_{s}}^{0} \frac{V_{in}}{L}dt = \frac{V_{in}D}{Lf_{s}}$$
これが、インダクタ電流リップルの式になります。インダクタンス・キャリア周波数が増加することで、リップルを抑制できることが分かります。
出力電圧のリップル量
キャパシタの電荷について、次の式が成立します。ただし、リップルとして変動量を知りたいので、電流の極性を調整しています。また、出力電流は一定と近似します。
$$ \Delta Q = C \Delta V$$
$$ \Delta Q = \int_{0}^{DT_{s}}I_{out}dt = \frac{D}{f_s}I_{out}$$
これらの式から次の式を導出できます。
$$ \Delta V_{out} = \frac{I_{out}D}{Cf_{s}}$$
シミュレーション結果とのリップル量比較
このリップルの式がシミュレーションと一致するか確認します。シミュレーションモデルとその結果は別ページにて紹介していますが、モデルはここに再掲します。ここでは、リップルに注目して理論式と一致しているか確認します。
Dutyを変更した場合のリップル量比較
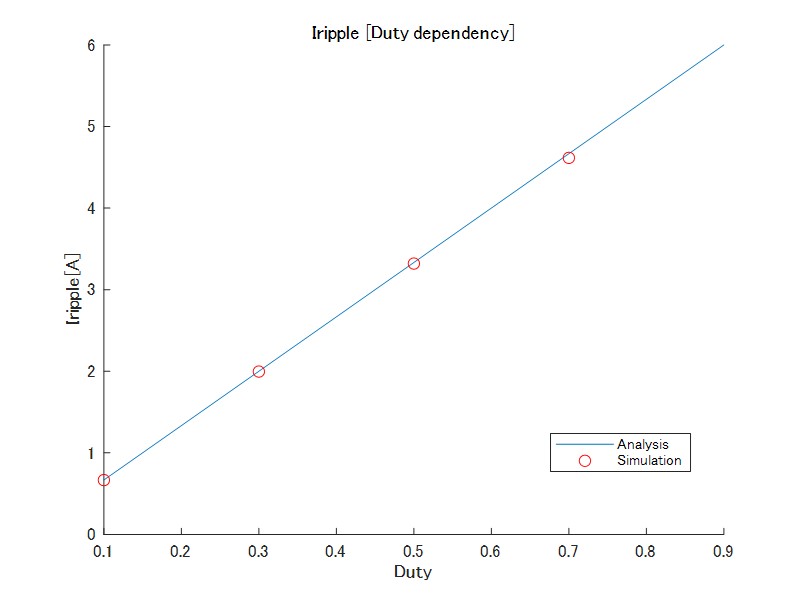
図2 インダクタ電流リップル(Duty依存性)
Dutyの増加に伴い、リップル量は線形に増加する
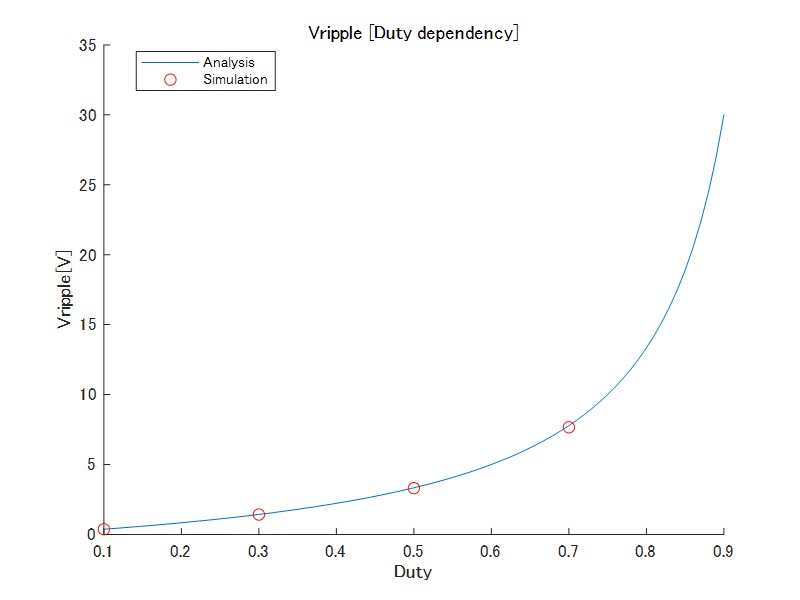
図9 出力電圧リップル(Duty依存性)
Dutyの増加に伴い、リップル量は増加する
Dutyを変更した場合のリップルの様子を図2図3に示します。インダクタ電流および出力電圧リップルは理論値と一致することが分かります。
キャリア周波数を変更した場合のリップル量比較
キャリア周波数を変更した場合のリップルの様子を図4図5に示します。インダクタ電流および出力電圧リップルは理論値と一致することが分かります。
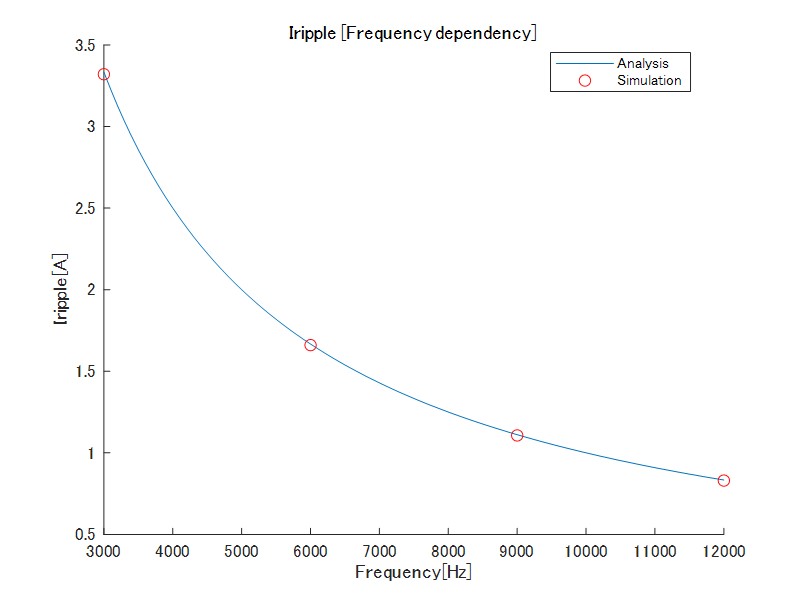
図8 インダクタ電流リップル(キャリア周波数依存性)
キャリア周波数の増加に伴い、リップル量は減少する
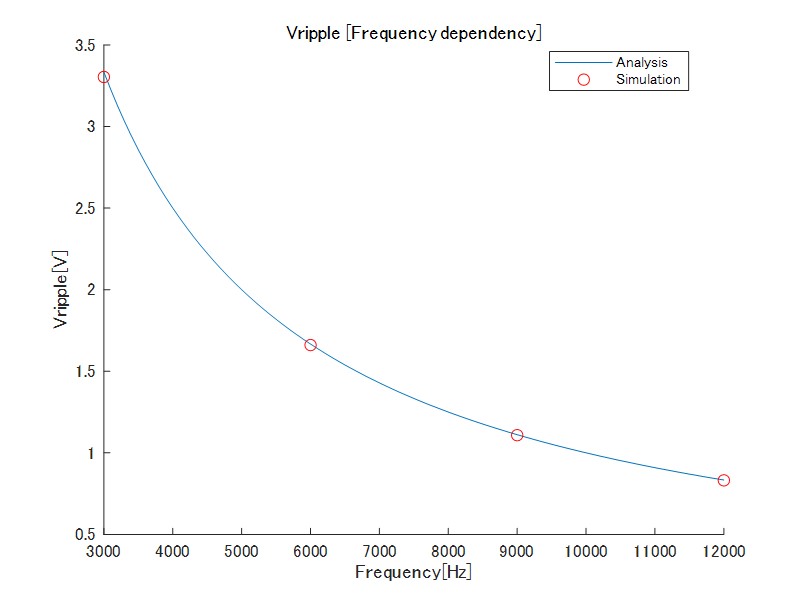
図9 出力電圧リップル(キャリア周波数依存性)
キャリア周波数の増加に伴い、リップル量は減少する
インダクタンスを変更した場合のリップル量比較
インダクタンスを変更した場合のリップルの様子を図6図7に示します。インダクタ電流および出力電圧リップルはほぼ理論値と一致することが分かります。
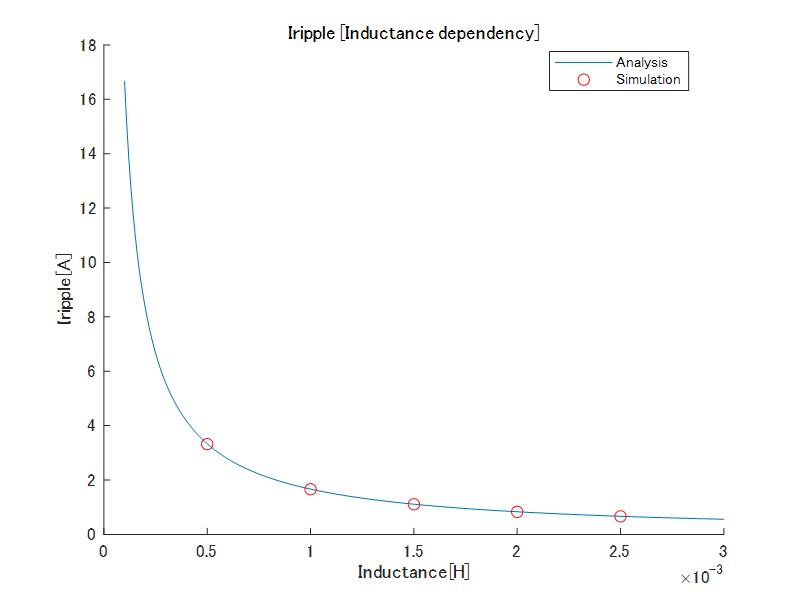
図8 インダクタ電流リップル(インダクタンス依存性)
インダクタンスの増加に伴い、リップル量は減少する
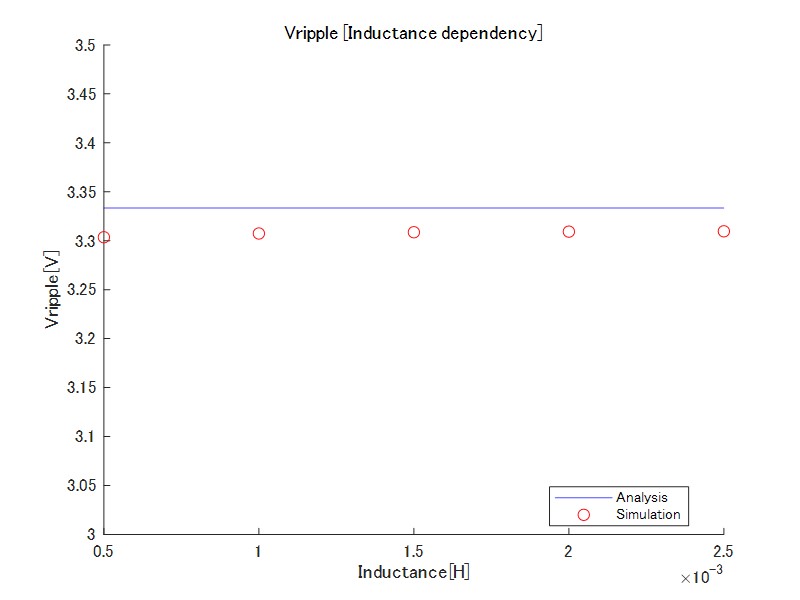
図9 出力電圧リップル(インダクタンス依存性)
リップル量はインダクタンスと無関係
キャパシタンスを変更した場合のリップル量比較
キャパシタンスを変更した場合のリップルの様子を図8図9に示します。インダクタ電流および出力電圧リップルはほぼ理論値と一致することが分かります。
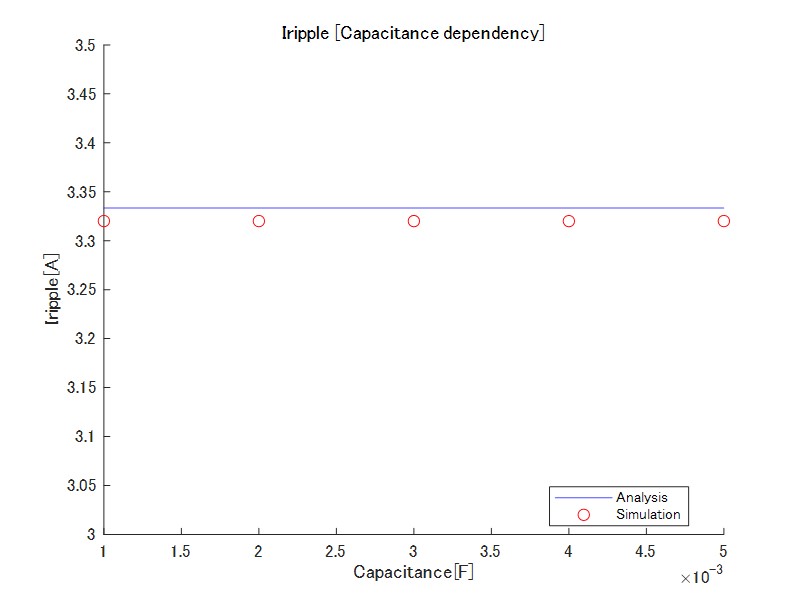
インダクタ電流リップルはキャパシタンスと無関係
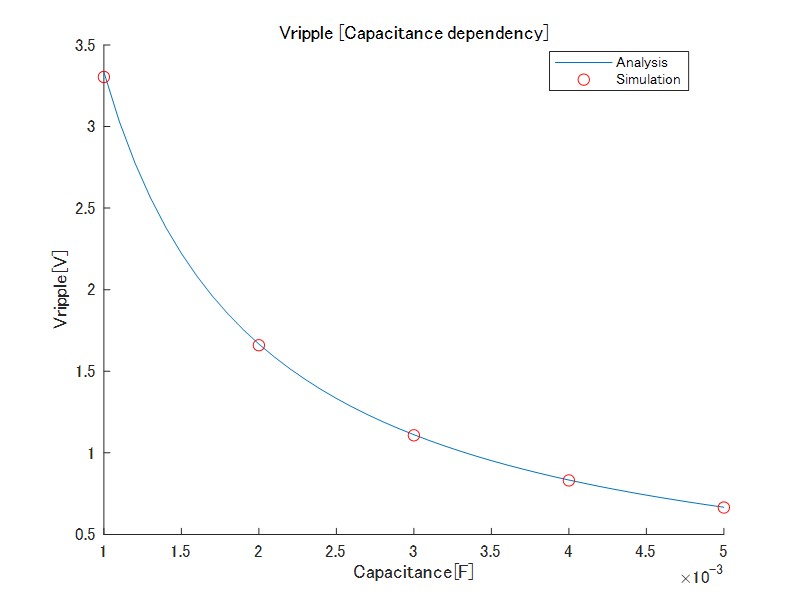
キャパシタンス増加に伴い、リップル量は減少する
まとめ
このページでは、昇圧コンバータのリップルについて紹介しました。ポイントは次のとおりです。
- インダクタ電流リップルはインダクタンスとキャリア周波数を増加させることで抑制することができます。
- 出力電圧リップルはキャパシタンスとキャリア周波数を増加させることで抑制することができます。


