降圧コンバータの出力波形を図1に示します。半導体スイッチを用いて矩形波を生成した後は、LCフィルタを通過させ、直流出力を生成します。このとき、直流出力は完全には平滑化できず、若干の振動成分を持ちます。この振動をリップルと呼びます。ここでは振動の大きさを抑制するためにどのような手法を取ればよいのか考察します。
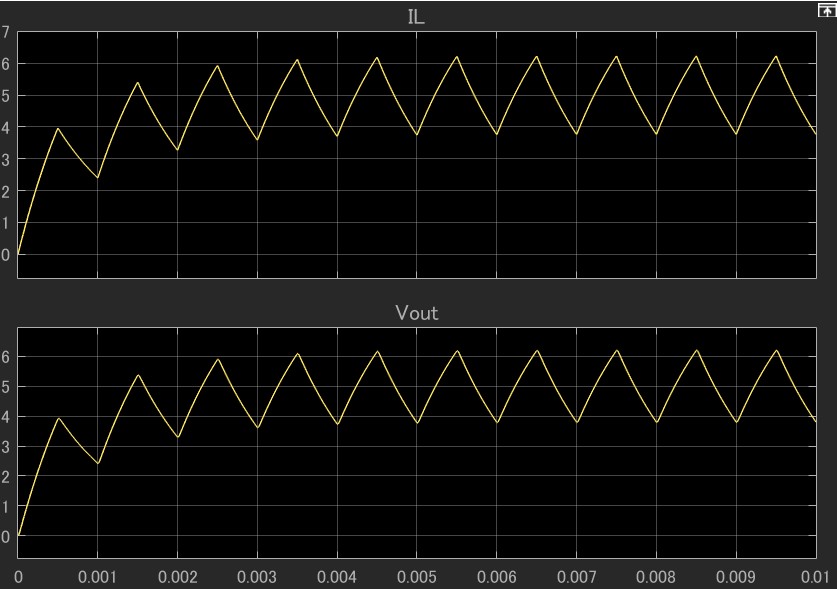
降圧コンバータのリップル
図2に改めて降圧コンバータの回路図を記載します。ここでは、インダクタ電流のリップルと出力電圧のリップルを考えます。インダクタ電流と出力電圧は微分方程式を解くことにより解析解を取得することが可能ですが、この時の解は複雑です。そのため、回路パラメータとリップルの関係を直感的に理解することが難しくなっています。
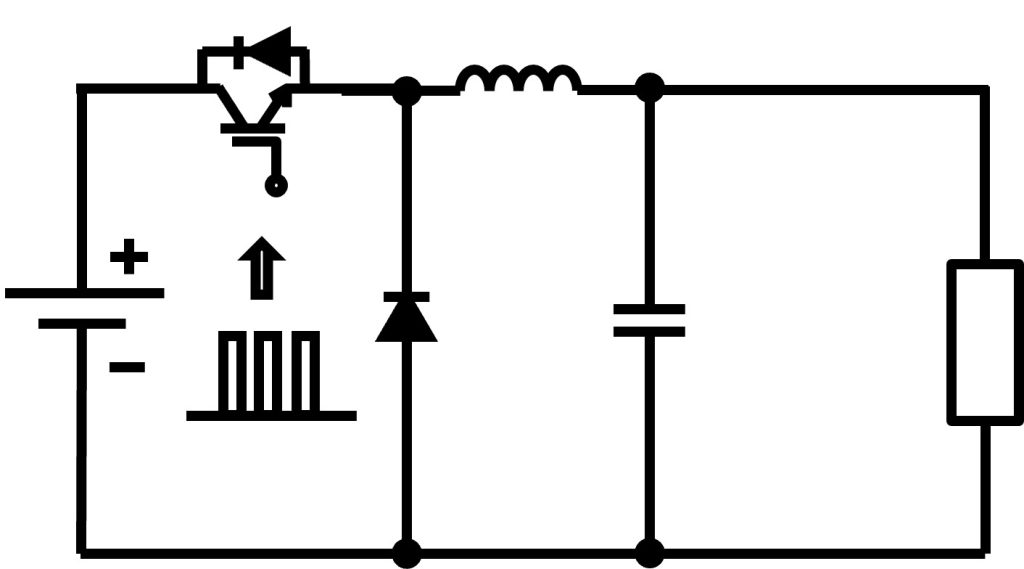
ここでは、出力電圧とインダクタ電流について、逐次近似法を利用し、振動のPeak to Peak値を概算します。 なお逐次近似法とは、初期値から計算を繰り返すことで数値解を得る手法です。その数式は次のようなものであり、繰り返し計算を行っていきます。
$$ x_0 (t) = c $$
$$ x_1(t) = c+ \int_{t_0}^{t}x_0(t)dt $$
$$ x_2(t) = c+ \int_{t_0}^{t}x_1(t)dt $$
逐次近似法によるリップル概算量の計算
繰り返しを行うことで、解が解析解に近づいていきます。降圧コンバータの振動量計算では、途中までの計算を利用し、その特徴を把握することを目的とします。
インダクタ電流と出力電圧の振動量計算
A) 初期値設定
まずはリップル=0の出力電圧を初期値と設定します。つまり以下の式が成立します。
$$ V_{out}^{(0)} = DV_{in}$$
次にこの時のインダクタ電流を計算します。
B) インダクタ電流の計算
スイッチオン状態とスイッチオフ状態で回路が変わります。インダクタ電流もスイッチオン状態とスイッチオフ状態で場合分けして考えます。
B-1) スイッチオンの時(0 < t < DTs)
スイッチオンの時、次の回路が成立します。
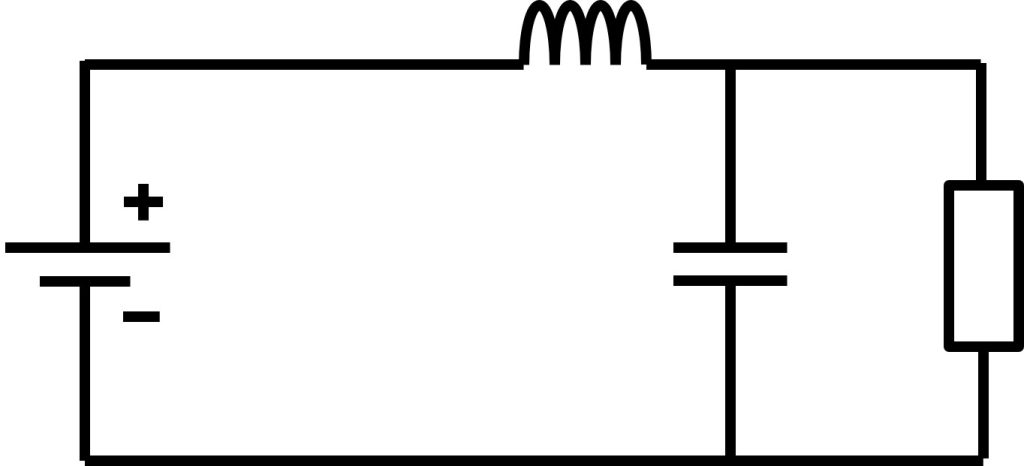
インダクタにかかる電圧について計算すると以下の式が成立します。
$$ L\frac{dI_{L}^{(0)}(t)}{dt} = V_{in}-V_{out}=V_{in}(1-D)$$
この式をインダクタ電流について解くと以下の式が成立します。
$$ I_{L}^{(0)}(t) = I_{L}^{(0)}(0) +\frac{V_{in}(1-D)}{L}t$$
この式から、オン状態においてインダクタ電流は直線的に変化することが考えられます。
B-2)スイッチオフの時(DTs < t < Ts)
スイッチオフの時、次の回路が成立します。
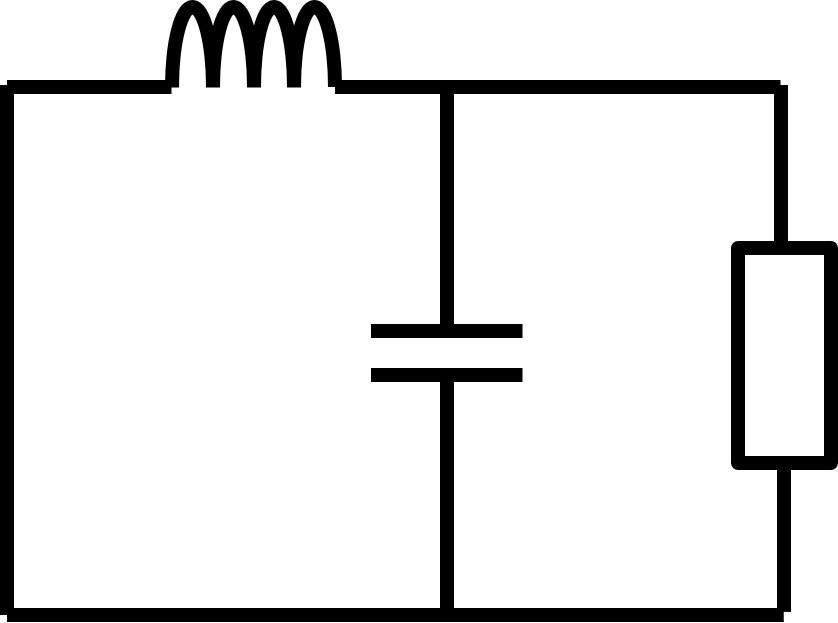
インダクタにかかる電圧について計算すると以下の式が成立します。
$$L\frac{dI_{L}^{(0)}}{dt}=-V_{out}=-DV_{in}$$
この式をインダクタ電流について解くと以下の式が成立します。
$$ I_{L}^{(0)}(t) = I_{L}^{(0)}(DT_{s}) +\frac{-DV_{in}}{L}t$$
この式から、スイッチオフ状態においてもインダクタ電流は直線的に変化することが考えられます。
A-3) インダクタ電流の平均値とリップル(Peak to Peak)値の算出
ここで、電流の平均値について考えます。出力電圧リップル=0を仮定するとき、コンデンサ電流=0となります。インダクタ電流の平均値は出力電圧値から計算でき、その時の時刻は、\( t = \frac{DT_{s}}{2}\)となります。
$$I_{L}(\frac{DT_{s}}{2}) =I_{L}(0)+\frac{(1-D)}{L}V_{in} \times \frac{DT_{s}}{2} = \frac{V_{in}}{R}$$
つまり
$$I_{L}(0) =\frac{DV_{in}}{R} -\frac{(1-D)DT_{s}}{2L}V_{in}$$
$$I_{L}(DT_{s}) = \frac{DV_{in}}{R} +\frac{(1-D)DT_{s}}{2L}V_{in}$$
以上から電圧リップルをゼロと仮定したときのインダクタ電流は次の図のような関係にあります。
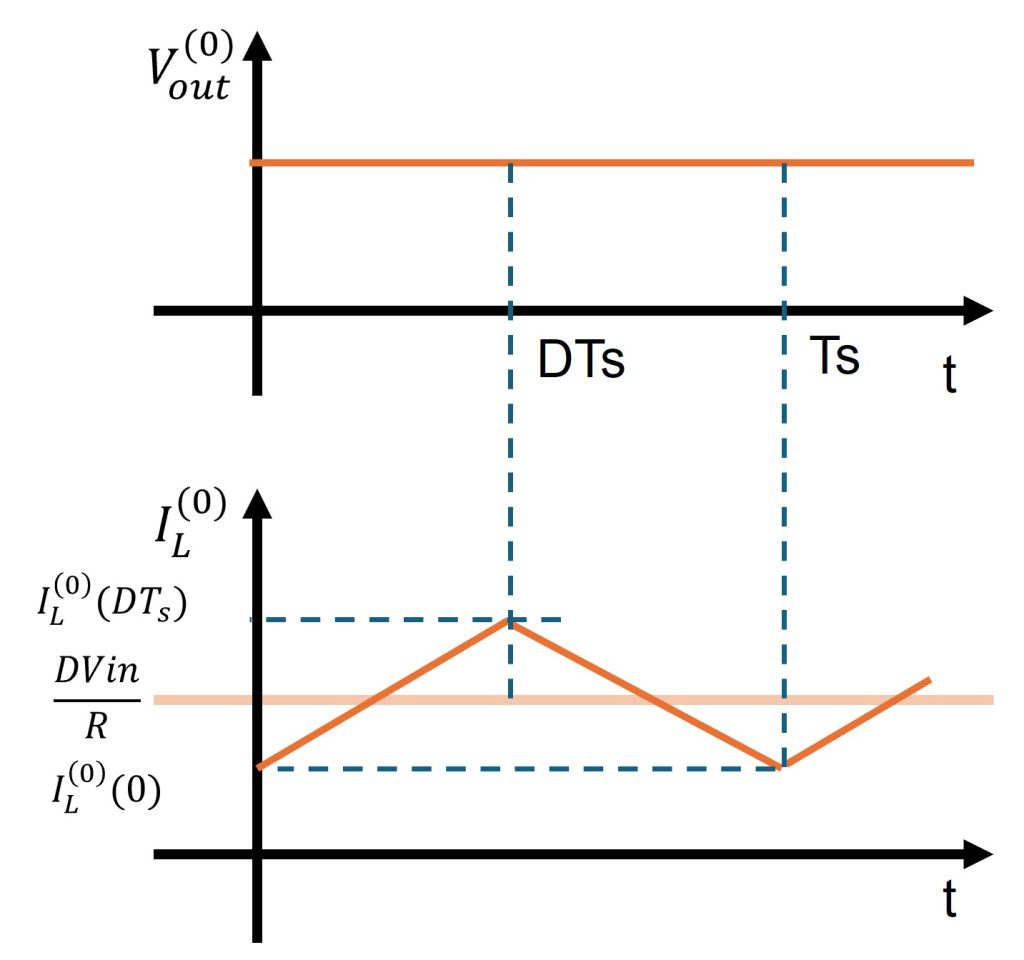
ここで、電流のPeak to Peakを計算します。グラフより、明らかにt=0にて最小値、\(t=DT_{s}\)にて最大値を取ります。この時の傾きと経過時間から以下の式が成立します。
$$ I_{p-p}^{(0)} =I_{L}^{(0)}(DT_{s})-I_{L}^{(0)}(0) = \frac{V_{in}(1-D)}{L}DT_{s}$$
従って電流リップルはキャリアサンプル時間に比例し(=キャリア周波数に反比例し)、インダクタンスに反比例することが分かります。
B)出力電圧のリップル(Peak to Peak値) 値の概算
インダクタ電流が計算できたので、出力電圧を更新します。コンデンサにかかる電圧について計算すると以下の式が成立します。
$$ V_{out}^{(1)}(t) = V_{C}^{(0)}(0)+\frac{\int_{0}^{t}(I_{L}^{(0)}(t)-I_{out}^{(0)})dt}{C}$$
ここで、\( \int_{0}^{t}(I_{L}^{(0)}(t)-I_{out}^{(0)})dt\)はインダクタ電流のグラフにおいて、斜線で示した面積に相当します。なので、電圧の概形は下のとおりとなります。(※電圧値は分かりやすく大げさに表現しています。)
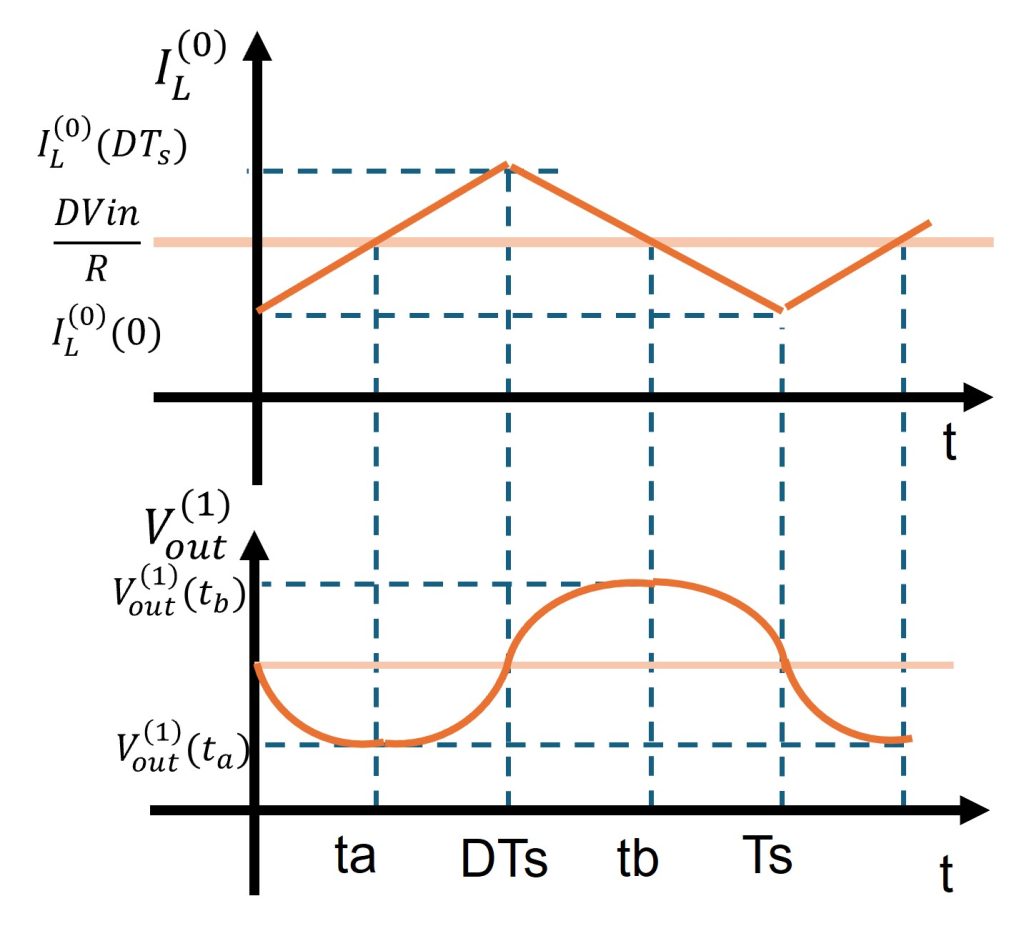
ここで、電圧のPeak to Peak値は次のとおりとなります。
$$ V_{out p-p}^{(1)} = V_{out}^{(1)}(t_{b})-V_{out}^{(1)}(t_{a})=\frac{\int_{t_{a}}^{t_{b}}(I_{L}^{(0)}(t) – I_{out}^{(0)})}{C}$$
また、積分値は、面積に相当します。底辺が(tb – ta)=Ts/2、高さがIp-p/2の三角形なので、上式は以下のように式変形できます。
$$ V_{out p-p}^{(1)} = \frac{1}{C} (\frac{1}{2} \times \frac{T_{s}}{2} \times \frac{V_{in}(1-D)}{2L} DT_{s}) = \frac{T_{s}^{2} V_{in}(1-D)D}{8CL}$$
従って出力電圧リップルはキャリアサンプル時間の二乗に比例し(=キャリア周波数の二乗に反比例し)、キャパシタンスおよびインダクタンスに反比例することが分かります。
まとめ
降圧コンバータのリップルについて、考え方を紹介しました。ポイントは以下のとおりです。
- 逐次近似法を用いて、インダクタ電流と出力電圧のリップルを概算しました。
- インダクタ電流はインダクタンス、キャリア周波数に反比例します。
- 出力電圧リップルはキャパシタンス、インダクタンス、キャリア周波数に反比例します。

