別ページにて、単相半波整流回路の動作を確認しました。その回路では、波形が汚い、平滑用コンデンサにパルス状の電流が流れ込むなどの問題が発生しました。この問題の原因として、交流電圧が負の時に何もできていない点にあります。この電圧が負の区間を有効活用するものが単相全波整流回路となります。
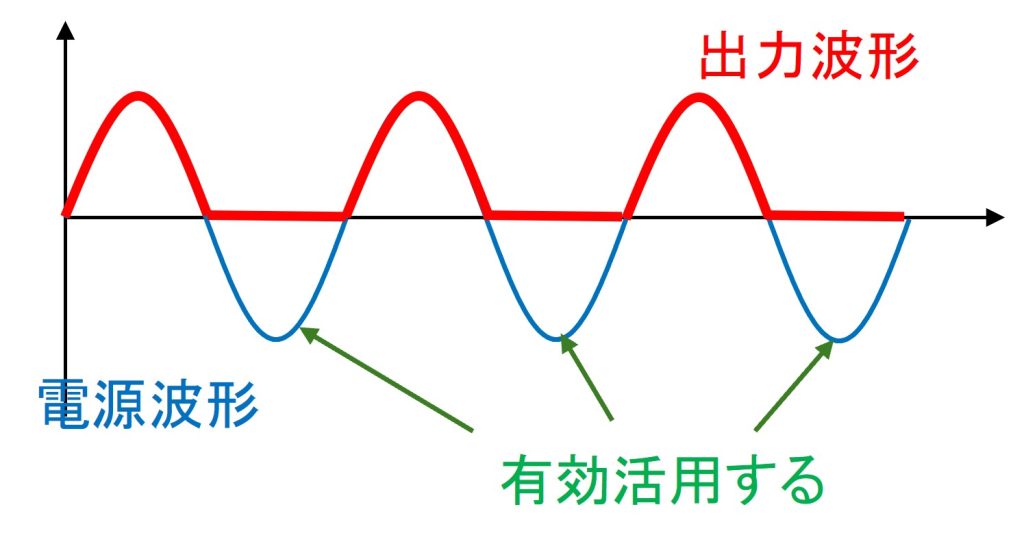
負の電圧の時の信号を利用できていないのがもったいない
複数ダイオードの動作
単相全波整流回路の説明の前に、ダイオードを複数接続したときのふるまいを確認します。ここでは2パターンの場合を考えます。
カソード側が同電位の場合
図2の回路を考えます。アノード電圧V1のダイオードD1とアノード電圧V2のダイオードD2がカソード側で接続されています。この時カソード電圧VRがどうなるかを考えます。ただし、V1>V2とします。
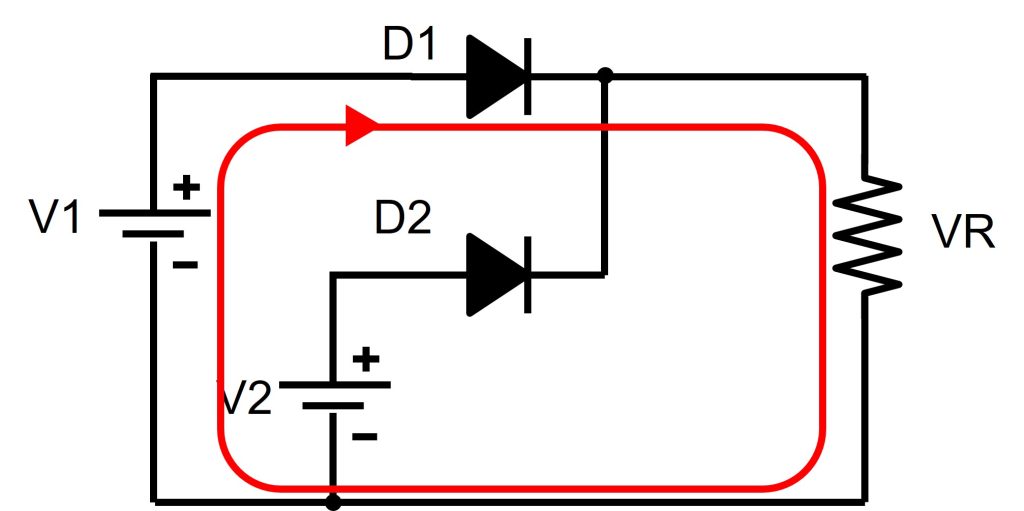
V1>V2であれば、抵抗にはV1が印加される
D1側回路が存在せず、ダイオードD2の電圧降下を無視すると、カソード電圧VRはダイオードD2のアノード電圧V2なります。
この状態からD1側の回路を接続するとどうなるか。ダイオードD1にとって、アノード電圧V1、カソード電圧V2という状態なのでダイオードD1は導通します。導通するということは、カソード電圧はダイオードD1の電圧降下を無視するとアノード電圧V1と一致することになります。
従って、複数のダイオードをカソード側で接続すると、最大値選択回路として動作をすることになります。
アノード側が同電位の場合
図3の回路を考えます。カソード電圧-V1のダイオードD1とカソード電圧-V2のダイオードD2がアノード側で接続されています。この時、アノード電圧がどうなるかを考えます。ただし、V1>V2とします。
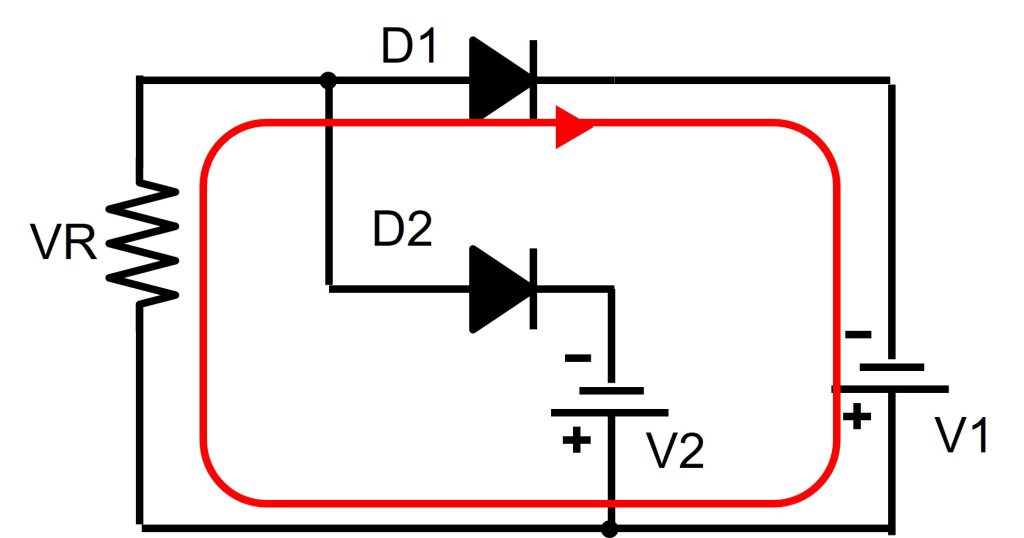
図3 アノード同電位の場合の回路動作
-V1<-V2であれば、抵抗には-V1が印加される
D1回路が存在せず、ダイオードD2の電圧降下を無視すると、アノード電圧VRはダイオードD2のアノード電圧-V2なります。
この状態からD1側の回路を接続するとどうなるか。ダイオードD1にとって、アノード電圧-V1、カソード電圧-V2という状態なのでダイオードD1は導通します。導通するということは、カソード電圧はダイオードD1の電圧降下を無視するとアノード電圧V1と一致することになります。
従って、複数のダイオードをアノード側で接続すると、最小値選択回路として動作をすることになります。
単相全波整流回路の回路構成と出力波形
単相全波整流回路の回路は図4のようになります。交流電源と負荷の間に4つのダイオードが配置されています。この回路の上側は先ほどの最大電圧選択回路に相当し、下側は先ほどの最小電圧選択回路になります。
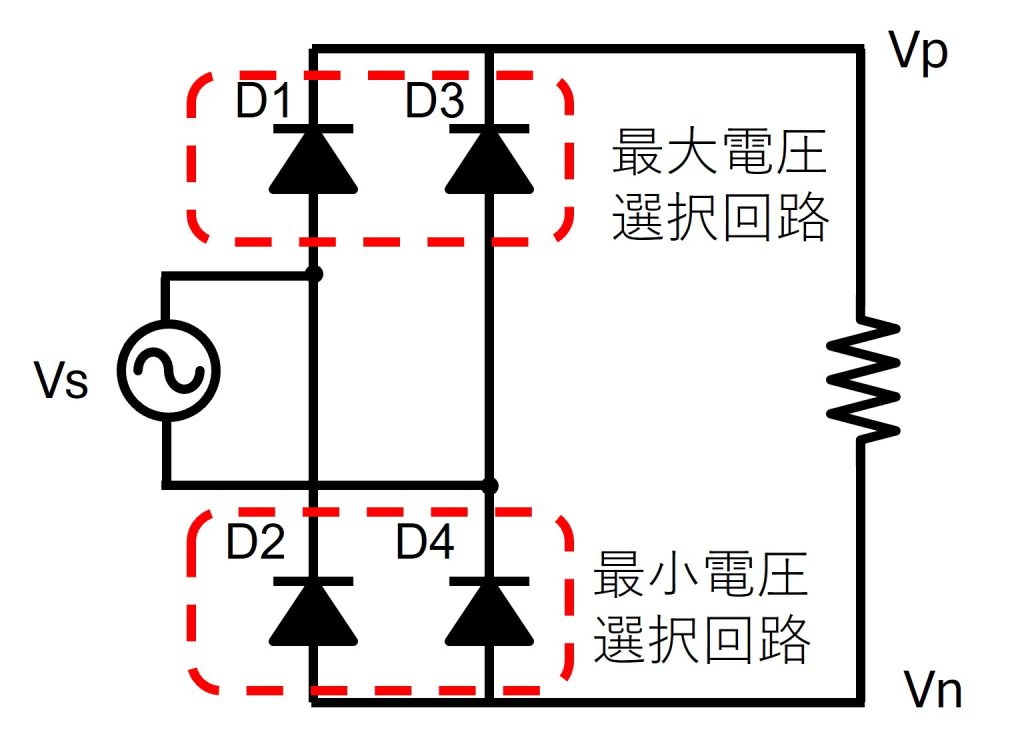
正側出力端子の電圧Vpは交流波形と電圧0[V]の最大値選択となるため、図5のとおり赤色の波形が出力されます。
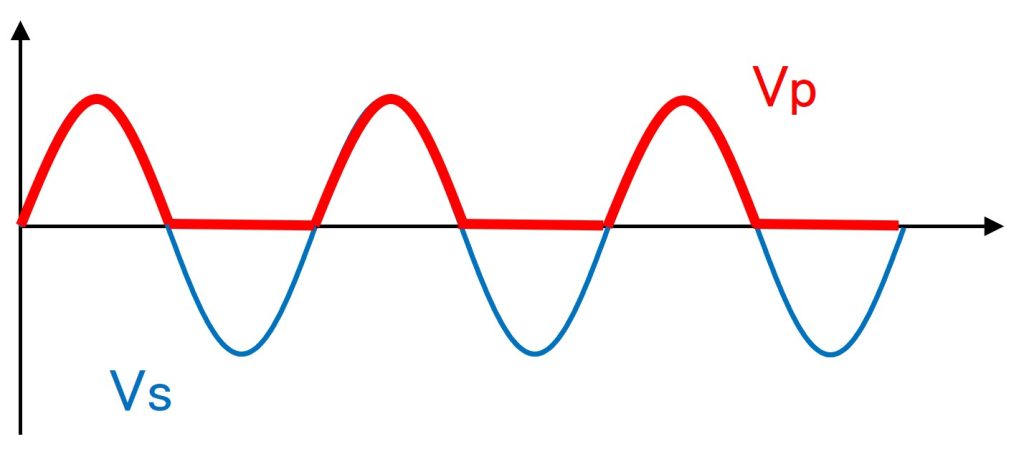
最大値選択回路により、交流波形と接地の最大値が選択される
負側出力端子の電圧Vnは交流波形と電圧0[V]の最小値選択となるため、図6のとおり緑色の波形が出力されます。

図6 負荷の負側端子の電圧波形
最小値選択回路により、交流波形と接地の最小値が選択される
出力の負荷抵抗にかかる電圧はこの二地点間の電圧なので図7のとおりとなります。これで、単相半波整流回路で無駄になっていた、負の電圧区間の電圧も有効活用できるようになります。
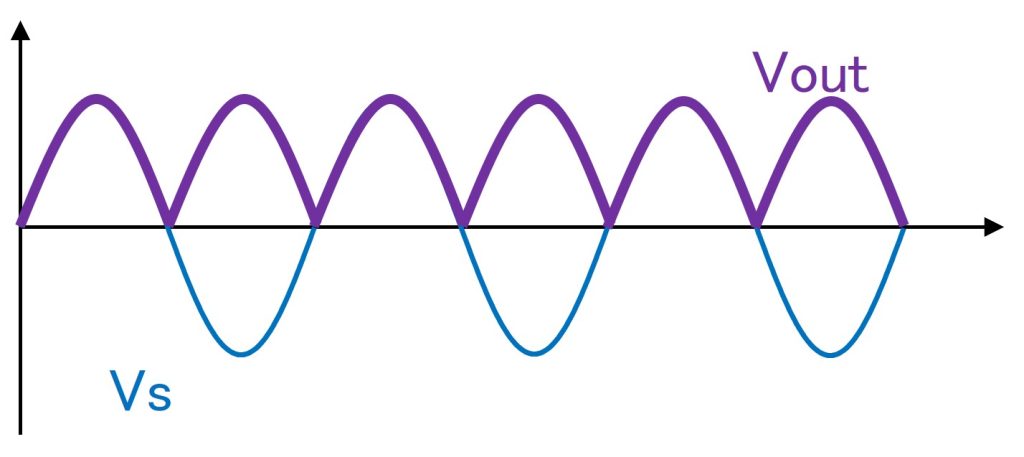
図7 負荷の電圧波形
正側端子と負側端子の差分が出力される
単相全波整流回路の電流経路
出力電圧が計算されましたが、どのタイミングでどのダイオードが導通しているか確認します。
最大値選択回路(D1,D3の導通)の導通タイミング
図5のとおり、交流電源がプラスの時、交流電圧を通過させます。つまり、図4のD1が導通します。交流電源がマイナスの時、電圧0[V]を通過させます。つまり図4のD3が導通します。
最小値選択回路(D2,D4の導通)の導通タイミング
図6のとおり、交流電源がプラスの時、電圧0[V]を通過させます。つまり、図4のD4が導通します。交流電源がマイナスの時、交流電圧を通過させます。つまり図4のD2が導通します。
以上の議論をまとめると、図8、図9のとおりの電流経路を導くことができます。
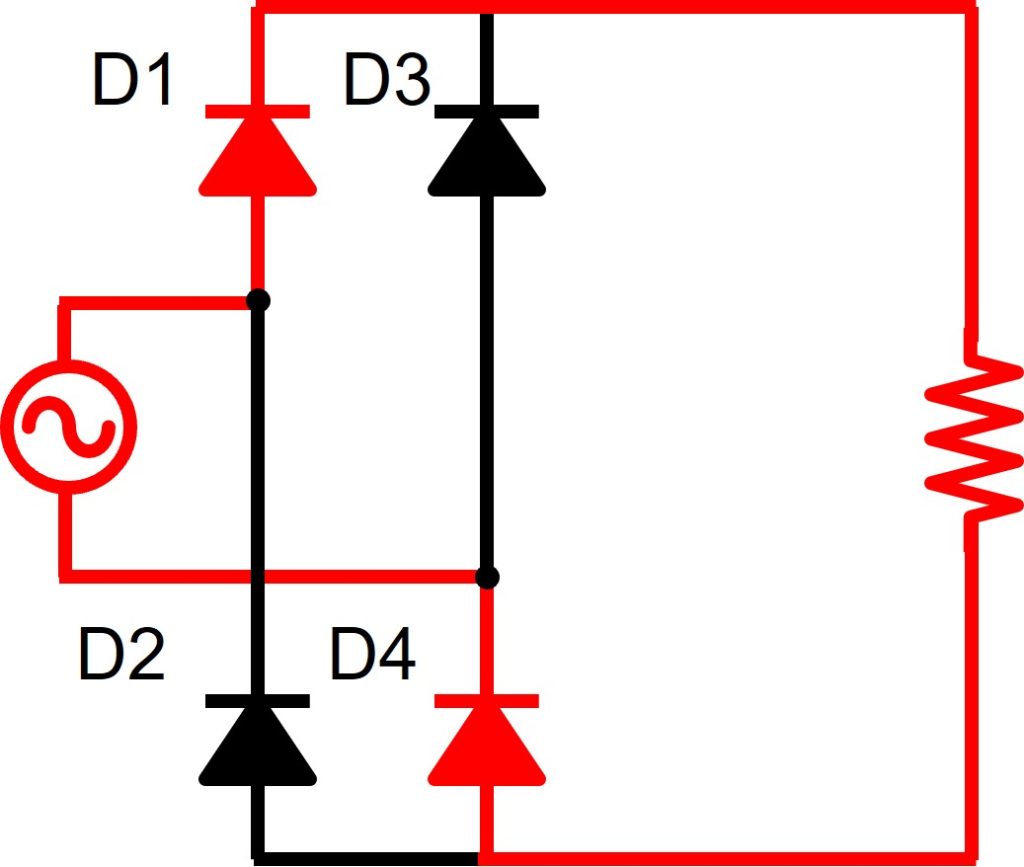
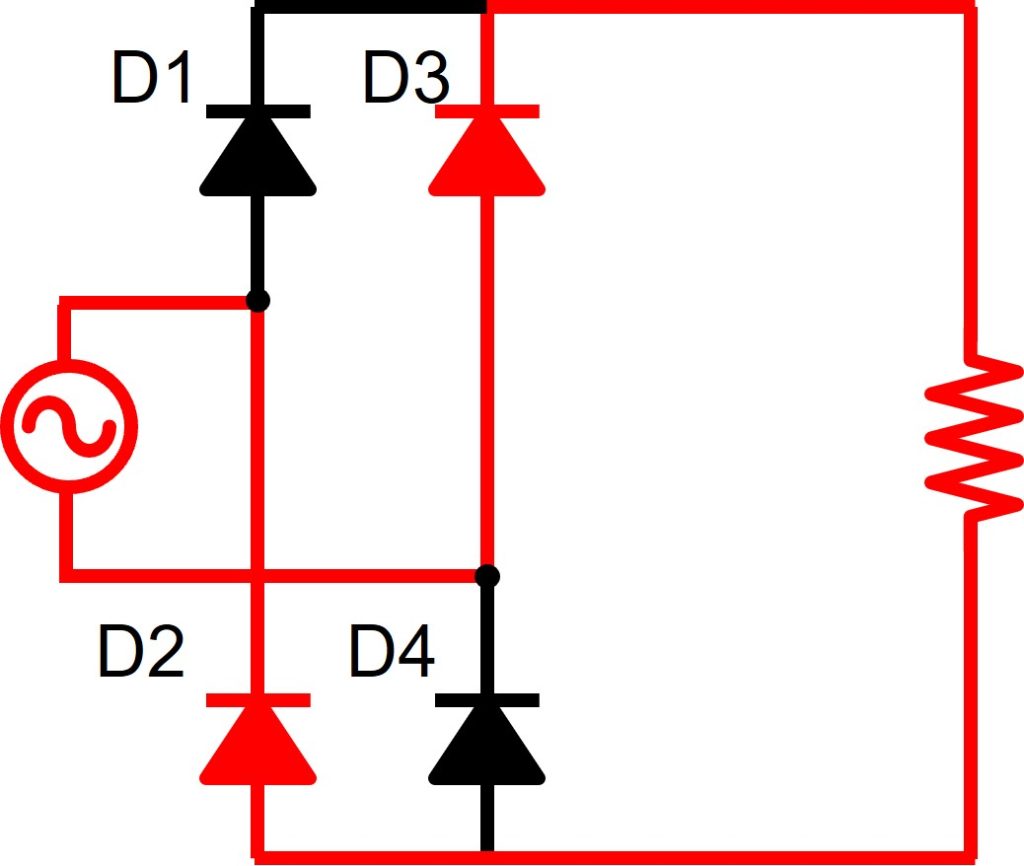
単相全波整流回路の出力電圧
単相全波整流回路の出力波形を導出できたので、出力平均電圧を導出します。電源電圧Vsは交流波形のため、電圧実効値Vを用いて、次の式で表せます。
$$ V_{s} = \sqrt{2}V \sin \theta $$
出力平均電圧Vdcは、1周期の電圧積分を1周期で割れば導出できます。単相全波整流回路の周期は図7の波形から\( [0, \pi] \)となります。したがって、平均電圧は次のとおりです。
$$ V_{dc} =\frac{1}{\pi} \int_{0}^{\pi} V_{load} d\theta =\frac{1}{\pi} \int_{0}^{\pi}\sqrt{2}V \sin \theta d\theta$$
この式を展開すると、直流電圧を得ることができます。
$$ V_{dc} = \frac{2\sqrt{2}}{\pi} V_{s}$$
つまり、交流実効値の約90%の直流電圧を得ることができます。
まとめ
このページでは、単相全波整流回路の動作原理を紹介しました。ポイントは以下のとおりです。
- 単相全波整流回路を用いることで、単相半波整流回路の問題点である波形を改善できます。
- 単相全波整流回路の回路構成、出力波形、電流経路を紹介しました。
- 単相全波整流回路を用いることで、交流電圧の約90%の直流電圧を得ることができます。


