さまざまな周波数のうち、高周波数信号のみを透過させるフィルタのことをハイパスフィルタといいます。このページでは、ハイパスフィルタの特性について、理論計算およびSimulinkを用いたシミュレーションを行い、詳細に理解していきます。
ハイパスフィルタの概要
ハイパスフィルタは、様々な周波数信号のうち高周波信号のみを透過させるフィルタになります。その動作イメージを図1に示します。
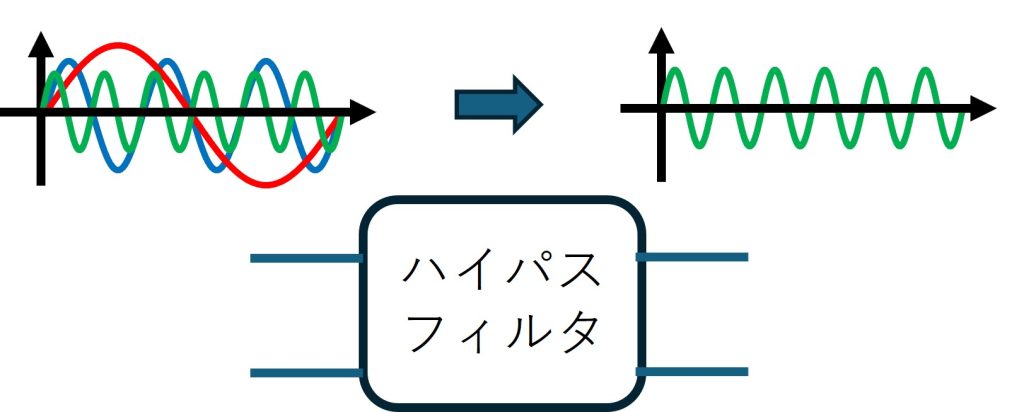
高周波信号は透過し、低周波信号は遮断する
図1では3種類の周波数の信号を入力し、最も高周波の信号のみを取り出しています。この時、どの周波数の信号を遮断するかはハイパスフィルタの設計で変更することができます。以下、ハイパスフィルタの詳細について考えていきます。
ハイパスフィルタの回路例
ハイパスフィルタの回路としては複数の種類があります。ここでは3種類の回路構成を紹介します。
CRフィルタ
ハイパスフィルタの代表的な回路がCRフィルタです。その回路図を図2に示します。
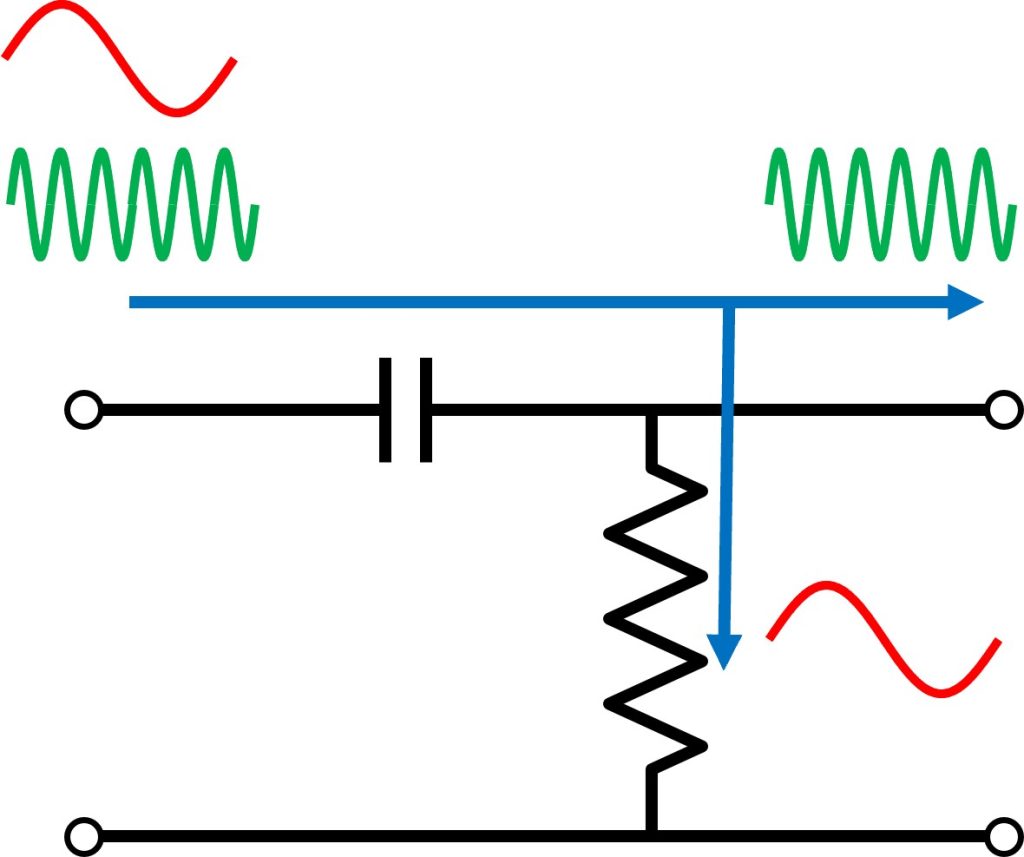
キャパシタのインピーダンスは低周波ほど小さいので、低周波ほどキャパシタにて阻止されるのが直感的にわかります。
CLフィルタ
ハイパスフィルタとしてCLフィルタも使われます。その回路図を図3に示します。

キャパシタのインピーダンスは高周波ほど小さいので、高周波ほどキャパシタ側に流れていくことが直感的にわかります。また、インダクタのインピーダンスは低周波ほど小さいので低周波ほど接地側に流れていくことが直感的にわかります。
これらの二重の効果のためフィルタの遮断性能はCRフィルタよりも優れています。
RLフィルタ
RLフィルタもハイパスフィルタとして動作させることが可能です。その回路図を図4に示します。
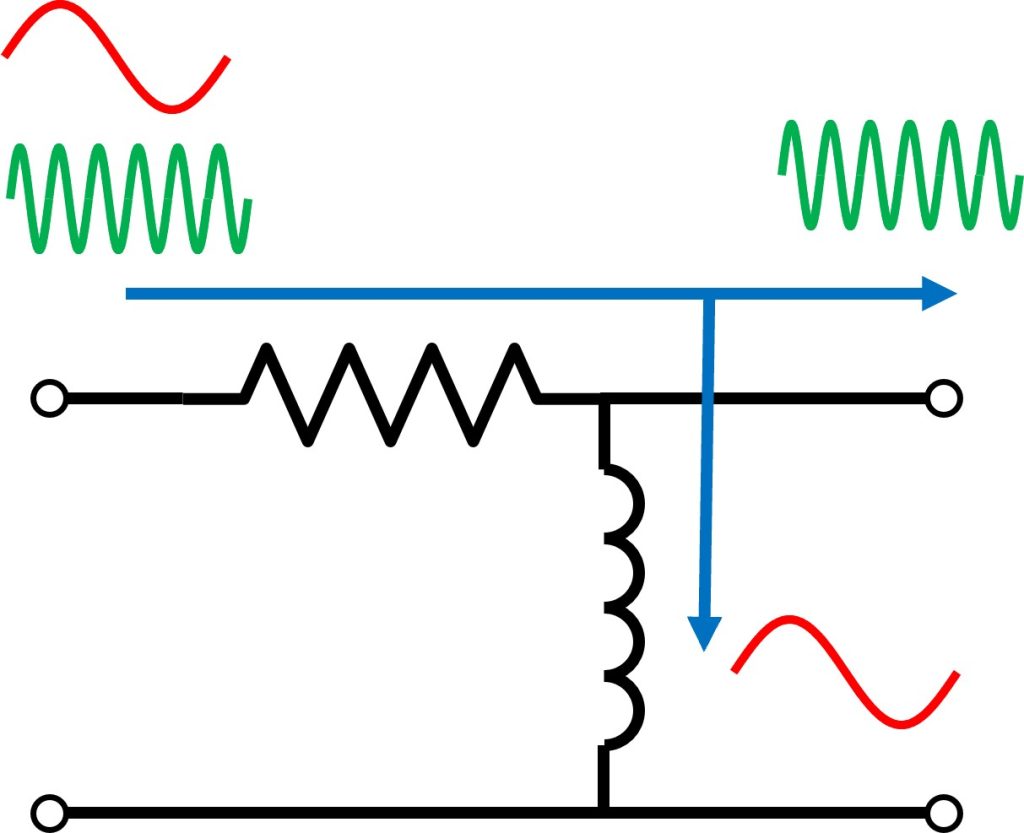
インダクタのインピーダンスは低周波ほど小さいので高周波ほど後段に流れていくことが直感的にわかります。
これらのフィルタのうち、ここではCRフィルタを取り上げ、その特性を理解していきます。他のフィルタについても同様の考え方で特性を導出できます。
CRフィルタの伝達関数とボード線図
CRフィルタの特性を導出するために、入力信号と出力信号の比(=伝達関数)を考えます。CRフィルタ回路にインピーダンスを書き込んだ回路図を図5に示します。
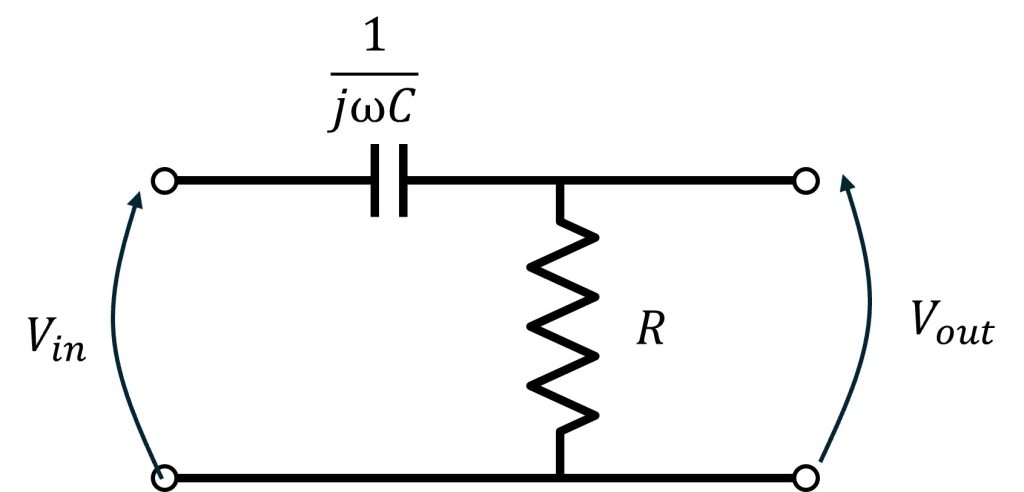
この回路図から伝達関数とボード線図を導出します。
CRフィルタの伝達関数の導出
インピーダンスの関係から、出力電圧は次のとおり計算することができます。
$$V_{out} = \frac{R}{\frac{1}{j \omega C} + R} = \frac{j \omega C R}{j \omega C R +1} V_{in}$$
入力電圧と出力電圧の比である伝達関数は次のとおりです。
$$\frac{V_{out}}{V_{in}} = \frac{j \omega CR}{1+j \omega CR}$$
この伝達関数からボード線図を導出します。
CRフィルタのボード線図の導出
入力と出力の比からボード線図を書きます。ボード線図はゲインと位相の周波数依存性を記述したものなので、ゲインと位相を計算します。
ゲインと位相の計算
伝達関数の分母に虚数単位があるため、分子側に持ってくるように式変形します。
$$\frac{V_{out}}{V_{in}} = \frac{j \omega CR}{1+j \omega CR} = \frac{j \omega CR(1-j \omega CR)}{1+(\omega CR)^2} = \frac{\omega CR(\omega CR + j)}{1+(\omega CR)^2} $$
従って、ゲインは次のように表せます。
$$ Gain = |\frac{V_{out}}{V_{in}}| = \frac{\omega CR(\omega CR + j)}{1+(\omega CR)^2} = \frac{\omega C R}{\sqrt{1 + (\omega C R)^2}}$$
また、ゲインが-3dB( \( \frac{1}{\sqrt{2}} \))になる角周波数(rad/s)は次のとおりです。
$$ \omega_c = \frac{1}{CR}$$
また、位相については次のとおりです。
$$ phase = tan^{-1} \frac{1}{\omega CR}$$
このゲインと位相をプロットしたものがボード線図になります。
MATLABによるボード線図のプロット
前述のGainとphaseを用いてボード線図を記述することができますが、MATLABでは伝達関数をベースにボード線図を書くことができます。
MATLABでは次のようなコードを書くことでボード線図を記述できます。https://jp.mathworks.com/help/control/ref/dynamicsystem.bode.html
H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
bode(H)第一行目はtf関数を用いて、伝達関数をHという変数に書き込んでいます。
第二行目にてbode関数を用いて、伝達関数をプロットするようにします。
次に実際にRCフィルタのボード線図を書いてみます。R=1Ωで固定し、C=0.1mF, 1mF, 10mFの3パターンでボード線図をプロットします。プロットした結果を図6に示します。
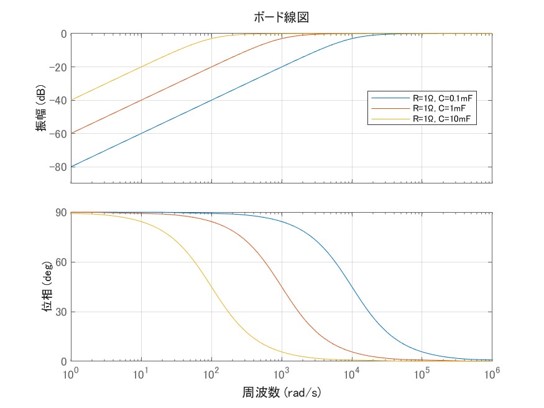
高周波のゲインが高く、低周波のゲインが小さい
いずれのプロットも高周波数側ではゲイン0(入力信号と等倍)であり、カットオフ周波数より小さい周波数でゲインが小さくなるプロットを示しています。カットオフ周波数はグラフから100rad/s, 1000rad/s, 10000rad/sとなりますが、これは1/CRの理論値と一致します。
Simulink・Simscapeを用いた周波数応答測定
CRフィルタは簡単な回路なため理論値を導出することが可能でしたが、複雑な回路では解析解を取得することが困難なことがあります。このような場合は、Simulinkの周波数応答測定機能を使うとボード線図を取得することができます。
ボード線図の取得方法はこのページやMathWorksのDocumentを参考にしてください。
周波数応答のオフライン推定
CRフィルタのSimscapeモデル
図7にSimscapeモデルを示します。
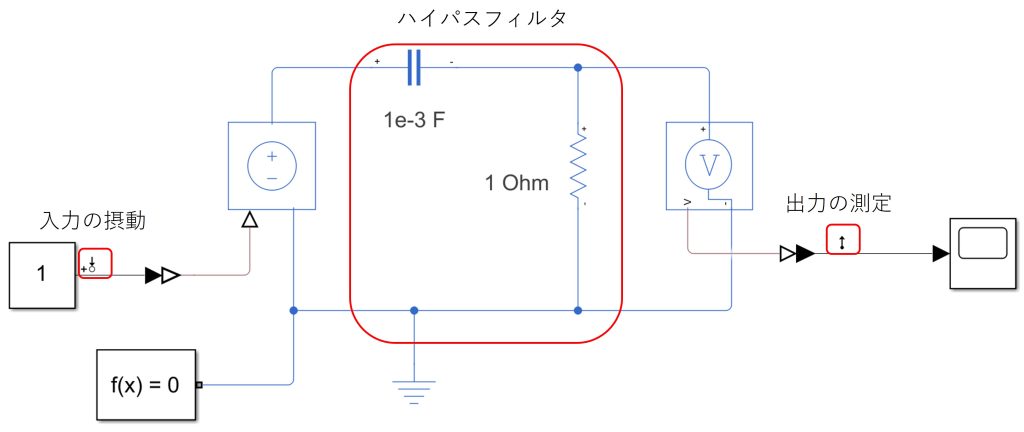
図2のようなCRフィルタに対して、Controlled Voltage Sourceブロックを追加しています。このブロックを追加することで周波数応答を測定することができます。なおフィルタのパラメータとしてはR=1Ω、C=1mFとしています。
このモデルに対して周波数応答推定器を活用してボード線図を取得します。
周波数応答推定の結果
各種設定をして周波数応答推定器を動作させて取得したボード線図が図8です。入力信号は1~10000Hz, 振幅は0.01に設定しています。(1Vの1%を与えています。)

低周波ほどゲインが小さくなり、ハイパスフィルタの特性を反映しているように見えます。この結果が解析解と一致するか確認します。
Simscapeによる周波数応答とMATLABによる解析解の比較
周波数応答推定器を活用してボード線図を取得できたので、この結果が理論値と一致しているか確認します。理論値とSimulinkによる周波数応答推定結果をプロットしたものを図9に示します。
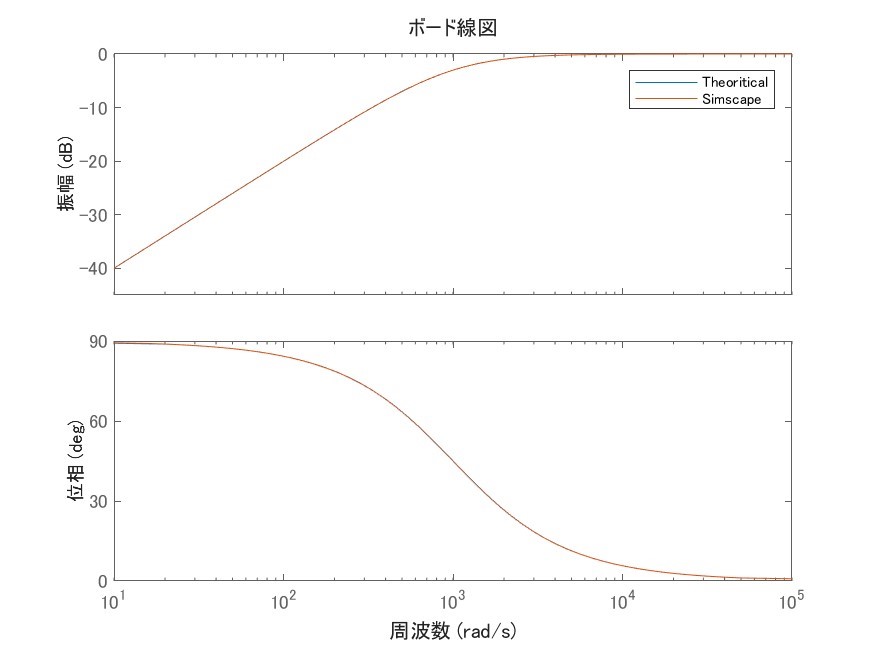
周波数応答推定結果(オレンジ色)は理論値(青色)と完全に一致していることが分かります。
周波数応答推定器を用いることで解析解を求めなくても周波数応答を取得することができます。(ただし、別ページにて発生しているように誤差が発生しうるので、過信はしないのが良いかと思います。)
まとめ
このページでは、ハイパスフィルタについて紹介しました。ポイントは次のとおりです。
- ハイパスフィルタとしてCRフィルタ、CLフィルタ、RRフィルタなどがあります。
- CRフィルタについて、伝達関数、ゲイン、カットオフ周波数、位相を導出しました。
- MATLABで伝達関数からボード線図を取得する方法を紹介しました。
- Simulinkの周波数応答推定器を利用してSimscapeモデルの周波数応答を推定しました。その結果、概ね理論値と一致したボード線図を取得することができました。

